9.10.2021
Ich werde hier erst einmal die Ergebnisse veröffentlichen, die ich schon vor langer Zeit auf ziemlich einfache Weise gewonnen habe. Es war früh in der ersten Hälfte der 2000er. Ich werde sie einfach aus meiner Präsentationsdatei nach hierher übertragen. Das Übersetzungsergebnis ist der Achsenkreis, in dem die partikulären -ismen nur noch als Universalismus, Totalitarismus und Partikularismus in Form der Pfeilgeraden vorkommen. Das jeweils gegenüberliegende kleinere Feld bzw. die dem kleineren Feld gegenüberliegende Pfeilgerade werden dem größerem Feld bzw. dem kleineren Feld tabellarisch zeilenmäßig untergeordnet. Wenn die jeweils kleineren Felder in der ersten Zeile stehen, wandern die größeren Felder ganz nach unten und wenn die reinen, nicht weiter unterschiedenen -ismen oben stehen, folgen in der nächsten Zeile die größeren Felder (Hauptfelder) und in der untersten die kleineren Felder (die Zwischenfelder). Alles ist irgendwann oben, in der Mitte oder unten. Schwierigkeiten können nur die partikulären -ismen bereiten, denn bei denen verschiebt sich die natürlich permutative Spalten-Reihenfolge, wie ich es schon bei meiner Erklärung der Gottes-Reihenfolge anhand der Allmacht, der Allgüte und des Allwissens kurz beschrieb. Ansonsten reicht tatsächlich das permutative Aneinanderreihen. „Das Ende der Geschichte“ sozusagen. 54 Gleichungen mit ihren Variablen besitzen wir so schon in grob-abstrakter Form. Das wird mir nicht reichen. Später dazu mehr. Ich hoffe, es hatte sich kein Fehler eingeschlichen. Bei den vielen Buchstaben durchaus möglich.









Die Gleichungen:



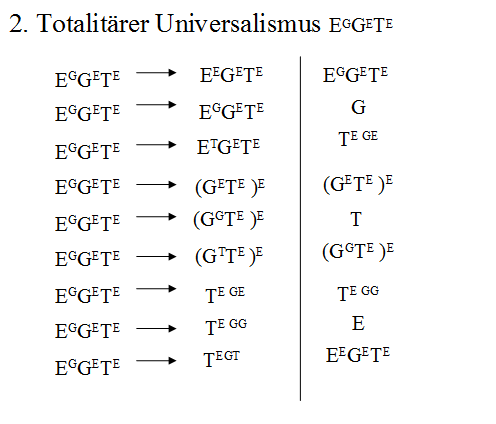

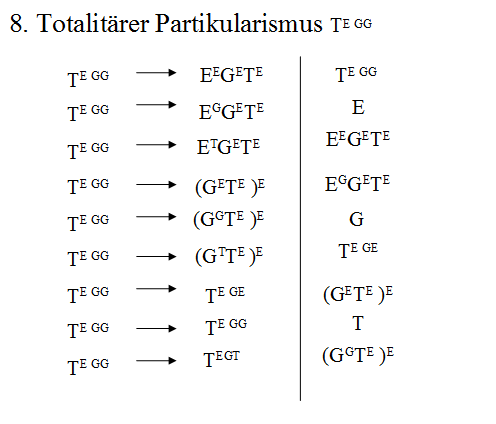
Eine Vorüberlegung
I. (6.12.2021)
Erst einmal sind die fehlenden 27 Gleichungen in ebenso grober Form leicht zu finden. Wenn Einheit, Ganzheit und Teilheit in die erste Zeile wandern. Doch das wären schon die Endlösungen und jede Endlösung ist von ihrer Anfangslösung verschieden. Und es gibt auch noch Zwischenschritte. Zwischenlösungen! Ich hatte schon auf einer anderen Webseite die physikalischen Bezüge zur „Einheit“(Theorie der starken Wechselwirkung), „Ganzheit“(Theorie der schwachen Wechselwirkung) und „Teilheit“(Theorie der elektromagnetischen Wechselwirkung) hergestellt. Die Kreise in den Graphiken stehen für die Einheit, der Untergrund(das Weiße im rechteckigen Rahmen) steht für die Ganzheit und die Buchstaben stehen für die Teilheit. Vielleicht können wir für Teilheit später noch eine elegantere Benennung einführen. Nun kann man von der Physik her den verschiedenen Wechselwirkungen ihre Eichbosonen zuordnen: Gluon(starke Wechselwirkung), W- und Z -Boson(schwache Wechselwirkung), Photon(elektromagnetische Wechselwirkung). Nach meinem Achsenkreis und meinen Theorien war es vorhersagbar, dass es an zweiter Stelle ein Dual geben muss(W und Z). Man kann also mit dem Achsenkreis nicht nur den Aufbau der Materie durch die Farbladungen bei den Gluonen logisch im Zusammenhang erfassen, sondern auch den Zusammenhang der Wechselwirkungen.
1. Hauptfeld: Starke Wechselwirkung(Gluon)
2. Hauptfeld: Schwache Wechselwirkung(W, Z)
3. Hauptfeld: Elektromagnetische Wechselwirkung(Photon)
Ich hatte ja schon kurz bei „Naturwissen“ angedeutet, dass die Naturwissenschaften die Gesetzmäßigkeiten der Genese liefern können: die Biologie jene für die Logik, die Chemie jene für die Ethik und die Physik jene für die Erotik. Also bezogen auf die Zeilen der Genese-Tabelle. Nun werden wir sehen, dass wir diese Zuordnungen auch für die Spalten vornehmen können. Denn für die physikalischen Gesetze brauchen wir die Felder der dritten Spalte(für die chemischen Gesetze also jene der zweiten und für die biologischen jene der ersten; „Leben“ wäre also ein Ergebnis der biologischen Gesetze, „Zeit“ jenes der chemischen Gesetze): Zeit, Werk und Raum. Nun gibt es in der Physik eine Dimensionsverwirrung. Eine Zeitdimension wird einfach als „vierte“ Dimension den drei Raumdimensionen dazugefügt. Schon interessant. Ob sich die Physiker klarmachen, was das bedeutet? Minkowski und so. Uns ist natürlich klar, dass die Zeit etwas Anderes als der Raum ist und selber drei Dimensionen besitzt: Vergangenheit, Gegenwart und Zukunft. Interessant wird es dann wieder beim Werk. Und durch die analytische Beschäftigung mit einem Dual eines Mittelfeldes können wir alle drei Felder weiter im Zusammenhang zueinander systematisieren. Natürlich meine ich Ursache und Wirkung als ersten Anfang.
II.(12.12.2021)
Für die Mathematik des Lichts reichen die einfachen Rechenoperationen der Schulmathematik nicht aus, sondern die Operation ist selber das Besondere, das Gesuchte. Welche Operationen finden wir in der Schulmathematik und gibt es verschiedene Stufen der Komplexität? Es gibt die Grundrechenarten: 1.Addition, das neutrale Element 0 und die Subtraktion, 2. Multiplikation, das neutrale Element 1 und die Division, 3. (Potenzierung:) Potenzen, Brüche und Wurzeln; Logarithmus; eine Einser-Potenz verändert nichts, eine Nuller-Potenz ergibt 1. Diese Reihe ist in sich abgeschlossen. Sie besteht aus drei Elementen. Beim ersten stehen sich Positives und Negatives noch gleichwertig gegenüber. Beim zweiten dominiert schon das Positive, denn Minus mal Minus ergibt Plus. Beim dritten hat das Positive sozusagen den „Sieg“ davongetragen, denn eine positive Basis können wir durch Potenzierung nicht in etwas Negatives verwandeln.
Dadurch wird auch gleich der Übergang zur zweiten Schicht der Rechenoperationen anschaulich. Man kann mit den Rechenoperationen der ersten Schicht keine Wurzel aus einer negativen Zahl ziehen. Dafür wurden die komplexen Zahlen mit ihrem imaginären Anteil geschaffen. Nun braucht man die Trigonometrie(oder die Eulersche Zahl mit einem Winkel in der Potenz). Zweite Schicht bedeutet auch, dass man für die Rechenoperationen der ersten Schicht die zweite Dimension nicht braucht. Für die Rechenoperationen der zweiten Schicht benötigt man sie. Die Rechenoperationen der zweiten Schicht: 1.(Trigonometrie:) Sinus, Cosinus, Tangens, 2. (Analysis:) Ableitung, Integral, Achsennullstellen, 3. (Vektorrechnung:) Vektoraddition(und -subtraktion), Skalarprodukt, Kreuzprodukt. Das Kreuzprodukt verweist schon auf die dritte Dimension, denn der Ergebnisvektor des Kreuzproduktes steht senkrecht zu den Ausgangsvektoren. Das Kreuzprodukt von zwei Vektoren zu bilden, bei denen eine gleiche Koordinate im dreidimensionalen Raum Null ist, ist aber möglich. Durch ein „Kreuz“-produkt in der zweiten Dimension erhalten wir rechnerisch einen Vektor. Dieser steht jedoch nicht senkrecht auf den Ausgangsvektoren. Das kann er nur im dreidimensionalen Raum.
Gibt es von der zweiten zur dritten Schicht weniger Abgeschlossenheit als von der ersten zur zweiten? Vielleicht kann man die imaginäre Zahl i ja als etwas Superpositives ansehen(vgl. den Übergang zur virtuellen Differenzierung)? Rechnerisch scheint aucht die zweite Schicht in sich geschlossen zu sein. Für die dritte Schicht brauchen wir dann die dritte Dimension. Zumindest zur Erklärung. 1. (die bestimmten Differentialoperatoren:) Gradient, Divergenz und Rotation. Die Differenzen können nicht in der Fläche selber entstanden sein, sondern die Fläche kann nur zur Darstellung dienen. Für die Unterscheidung des zweiten und dritten Elements der dritten Schicht reichen meine Mathekenntnisse zur Zeit noch nicht ganz aus. Ich kann sie auch nicht bezüglich möglicher Binnenelemente, den Hauptoperationen bzw. Hauptbedingungen näher bestimmen(vorher alles richtig?). Mathematiker mit einem Hochschulabschluss dürften hier weniger Schwierigkeiten haben. Das hält mich natürlich nicht auf. Ich muss nur logisch vorgehen und richtig anfangen. Das zweite Element der dritten Schicht hat auf jeden Fall mit Topologie zu tun und das dritte Element mit dem Wiedereintritt in den gleichen Raum bei dessen Verlassen(unberandete Sphäre). Damit wären dann die drei Schichten komplett und wir hätten den drei Dimensionen des Raumes Rechnung getragen.
Aber nur mit einem Verweis auf das Nächste, auf das Gefilde von Ursache und Wirkung, denn Ursache und Wirkung bedeutet, dass man nicht als der Gleiche wieder den Raum betritt, den man als derselbe verlassen hat(„second time around doesn‘t seem the same to me“, eine Band aus den 80ern). Zwar spielt die Zeit hier hinein. Aber dass das Nächste hier die Zeit ist, ist ein Trugschluss, denn mit dem Nächsten, dem Werk, muss auch das Dritte schon auftauchen. Das Dritte, die Zeit folgt aber erst nach dem Werk. Die Mathematik geht die Dinge nicht (oder nicht unbedingt) nach ihrer genetischen Reihenfolge an. Mathese ist etwas anderes als Genese. Dazwischen liegt noch die Poiese. Rein sprachlich, semantisch können wir zur Ursache ihre zugehörigen Reihenelemente leicht bilden: die Sache und die Endsache. Also wenn die Ursache eine Kraft ist, die auf eine Sache im Ruhezustand, zum Beispiel eine Metallkugel wirkt, so wird diese so weit fliegen bis alles wieder in Ruhe ist, ein Ruhezustand hergestellt ist. Also muss sich die Wirkung zwischen der Sache im Ruhezustand, oder im relativen Ruhezustand, und der Endsache, die selber wieder ein Ruhezustand (oder ein begrenzter Ruhezustand) in sich selber ist, befinden.
Was befindet sich dann aber zwischen Ursache und Sache und können wir das nicht gerade umkehren: also die Endsache in die Sache übersetzen? Mit dem Ergebnis der Ursache. Das Ganze nur durch eine Mathematik des Lichtes erfassen? Das Dritte, die Zeit taucht schon mit dem Zweiten auf – als grobes Abstraktum. Die Zeit ist das Letzt-Teilbare, das Letzteinheitgebende der elektromagnetischen Wechselwirkung. Der Raum ist eine Einheit. Durch die Quantenwelt ein einziger Homöomorphismus? Der Raum ist das Letzteinheitgebende der Starken Wechselwirkung. Dann ist das Werk das Letzteinheitgebende der Schwachen Wechselwirkung. Das Werk ist eine Ganzheit. Ein Buch braucht einen Autor und einen Leser, auch wenn der Autor der einzige Leser sein sollte. Werke besitzen desto mehr „Gewicht“, je mehr „Ein-Druck“ sie auf uns machen.
III.(22.12.2021)
Ich will diese Vorüberlegung mit einigen Erläuterungen abschließen, die vielleicht unnötig sind. Weil diese durch das Modell nahegelegt werden. Auch im Minkowski-Diagramm gibt es durch die Parallelen zu den Achsen eine Gleichortigkeit und eine Gleichzeitigkeit. Bzw. diese werden dort behauptet. Bei den Größen wird bei Minkowski & Co. etwas getrickst. Sein Diagramm scheint auch gut zur Veranschaulichung zu dienen. Dann bräuchte man ja nur noch eine Achse mehr und man hätte ein dreidimensionales Raum-Werk-Zeit-Diagramm!? Brauchen wir noch mehr?
Wodurch können wir uns die obigen neun „Elementoperationen“ vom Universalen Universalismus bis zum Partikulären Partikularismus begrifflich weiter erschließen? Wir besitzen die Bilder des Modells mit ihren Grundeinheiten und die zugehörigen Variablen – anscheinend mathematisch verknüpft. Eine Tabelle besteht ja auch aus x(Spalten) mal y(Zeilen) Feldern. Also besäßen wir mit den drei Grundvariablen Einheit, Ganzheit und Teilheit im Grunde eine dreidimensionale Tabelle. Ich ersetzte schon früher Teilheit durch Einzelheit und bin mit dieser Substitution immer noch zufrieden. Ich werde trotzdem weiter der Einfachheit halber vorübergehend von Teilheit sprechen. Aber was bedeuten die Potenzierungen mit der Einheit, der Ganzheit und der Teilheit? Wir haben schon der Anschaulichkeit halber den einfachen Bezug der Einheit zum Raum, der Ganzheit zum Werk und der Teilheit zu der Zeit hergestellt. Also können wir bei der Potenzierung jeweils drei Aspekte unterscheiden: gleich-, verschieden- und eigen-.
- E hoch E(Einheit hoch Einheit)=Gleichortigkeit
- E hoch G(Einheit hoch Ganzheit)= Verschiedenortigkeit
- E hoch T(Einheit hoch Teilheit)= Eigenortigkeit
- G hoch E(Ganzheit hoch Einheit)= Gleichgewichtigkeit
- G hoch G( Ganzheit hoch Ganzheit)= Verschiedengewichtigkeit
- G hoch T (Ganzheit hoch Teilheit)= Eigengewichtigkeit
- T hoch E(Teilheit hoch Einheit)= Gleichzeitigkeit
- T hoch G(Teilheit hoch Ganzheit)= Verschiedenzeitigkeit
- T hoch T(Teilheit hoch Teilheit)= Eigenzeitigkeit
Also könnte man theoretisch die obigen neun Elementoperationen durch die entsprechenden 3 mal 3 mal 3-Tabellen darstellen?
- den Universalen Universalismus durch die drei Achsen Gleichortigkeit, Gleichgewichtigkeit und Gleichzeitigkeit
- den Totalitären Universalismus durch die drei Achsen Verschiedenortigkeit, Gleichgewichtigkeit und Gleichzeitigkeit
- den Partikulären Universalismus durch die drei Achsen Eigenortigkeit, Gleichgewichtigkeit und Gleichzeitigkeit
- den Universalen Totalitarismus durch die drei Achsen Gleichgewichtigkeit, {Identität von Gleichgewichtigkeit und Gleichzeitigkeit} und Gleichzeitigkeit
- den Totalitären Totalitarismus durch die drei Achsen Verschiedengewichtigkeit, {Identität von Verschiedengewichtigkeit und Gleichzeitigkeit} und Gleichzeitigkeit
- den Partikulären Totalitarismus durch die drei Achsen Eigengewichtigkeit, {Identität von Eigengewichtigkeit und Gleichzeitigkeit} und Gleichzeitigkeit
- den universalen Partikularismus durch die drei Achsen {Identität der Alterität der Gleichzeitigkeit}, {Alterität der Gleichzeitigkeit} und Gleichzeitigkeit
- den totalitären Partikularismus durch die drei Achsen {Alterität der Alterität der Gleichzeitigkeit}, {Alterität der Gleichzeitigkeit} und Gleichzeitigkeit
- den partikulären Partikularismus durch die drei Achsen {Proprietät(?) der Alterität der Gleichzeitigkeit}, {Alterität der Gleichzeitigkeit} und Gleichzeitigkeit
Die Achsen der ersten drei Elementoperationen waren noch einfach zu bestimmen. Dann wurde es schon schwieriger. Ein Akt der letzten 10 Minuten(19.27). Fürs Erste. Ich werde es erst einmal damit bewenden lassen.
Zum Schluss noch ein kleiner schockierender Verweis auf den „Mathematischen Kurzschluss der Physik“. Wenn man die Physik (oder den Kern der Physikerkenntnisse) als eine Ansammlung von bisher fruchtbar gebrauchten Gesetzen versteht, die uns die physikalische Welt zu erklären helfen, wie viele davon sind direkt oder indirekt physikalische Ausdrücke des Mathematischen? Ich bin kein gelehrter Mathematiker oder Physiker. Ich habe diesen Kurzschluss auch noch nirgendswo gefunden. Es ist aber so auffällig, dass es eigentlich nicht übersehen werden kann (und auch noch kein Physiker und Mathematiker übersehen hat?). Die Kreisfläche wird errechnet durch das Produkt von Pi mal der zweiten Potenz des Radius. Die Energie wird nach Einstein(oder eher Poincaré?) berechnet durch das Produkt der Masse mal der zweiten Potenz der Lichtgeschwindigkeit. Also was für die Mathematik Pi ist, das Runde sozusagen, wird für die Physik die Masse sein, die Planeten und Sterne sozusagen. Und was ist nach dem Urknall im All verteilt? Energie. In der Mathematik idealisiert die homogene Kreisfläche. Und was durchquert das All bis zu dem Punkt des Unerkennbaren? Licht. Der Radius des Kreises. Unredlich? Vielleicht. Aber sicher nicht unwahr. Die analogische Qualität dieser Gleichsetzung(„Äquivalenz“?) kann kaum bestritten werden.
Nun, welche Einheiten braucht die Physik unbedingt: Längenmaß, Zeitmaß und Gewichtsmaß. Noch mehr? Wenn Pi die mathematische Blaupause der physikalischen „Masse“ ist, dann müsste die Eulersche Zahl die mathematische Blaupause für die „Länge“ sein und welche Zahl ist die mathematische Blaupause für die Zeit? Eins, negative und positive Ganzzahligkeit? Warum erkennen wir überhaupt? i hoch i ist eine bestimmbare Zahl! Aus dieser Verwirrung muss man erst einmal herauskommen. Genauso wie die Physik aus ihrer „Trägheit“!!
Die Jahns‘ sche Zahl j
23.3.2022(erst um 01.22 Uhr in der Nacht abgeschlossen; schon der 24.3.2022)
Die bedeutendsten bekannten mathematischen Konstanten sind wohl die Kreiszahl Pi und die Eulersche Zahl e. Über diese beiden erhalten wir für i hoch i eine konkrete Zahl. Wie ich schon schrieb, besitzen diese Konstanten auch bestimmte Bedeutungen für das Werk(im Falle von Pi) und für den Raum(im Falle von e). Nun fehlt noch die Zahl mit einer bestimmten Bedeutung für die Zeit. Oder besteht das Besondere der Zeit gerade darin, dass es auf ihrem Territorium so etwas gerade nicht gibt, sondern verschiedene oder sogar unbegrenzte Möglichkeiten? Nach dem Achsenkreis gibt es genau drei Hauptzahlen. Und insgesamt sechs feldmäßig. Mit den Zwischenfeldern. Wenn Pi und e so zugeordnet werden können, dann wären sie zwei dieser drei Hauptzahlen. Beide lassen sich durch Kettenbrüche jeweils mit 3 als erstem Summanden vor dem Kettenbruch konstruieren(bei e wird von 3 substrahiert).
Schon auf den ersten Blick fällt auf, dass e ungefähr den doppelten Abstand zur 3 besitzt wie Pi. Die dritte Hauptzahl liegt durch den geschlossenen Achsenkreis zwischen zweiter und erster Hauptzahl. Der Abstand zur 3 muss bei der dritten Hauptzahl noch geringer sein als bei Pi, wenn es einen Fortschritt von der ersten zur dritten Hauptzahl geben soll. Er muss ungefähr die Hälfte des Abstandes von Pi zur 3 betragen und dieser Betrag muss von der 3 substrahiert werden. Also besteht schon über die Zahl eine ungefähre Klarheit, ohne dass man sie schon durch einen Kettenbruch konstruiert hätte. Was aber möglich sein muss. Die Zahl mit zwei Nachkommastellen: 2,92……….. . Knapp unter 2,93. Das ist keine große Kunst. Ob es genau äquidistantiell ist: 2,929937241… ? Insofern noch niemand dieses eigentlich jedem Mathematiker bekannte Territorium für sich in Besitz genommen hat, setze ich mein j vor diese äquidistantiell zwischen e und Pi liegende Zahl[siehe dazu das P.S. zu diesem Text, 24.3.2022]. Aber vielleicht ist (Pi +e) durch 2 zu einfach.
Dementsprechend muss der erste Summand des ersten Nenners des Kettenbruches eine 12 (oder 12+1) und keine 6 sein. Also auf die Zwölf kommt es an. Wo bekommen wir die Zwölf her? In meiner SEX-fas-REX-ius-LEX-mos-SEX-usw.-Theorie(SEfaREiuLEmo-Theorie) erhielten wir die 6 beim Kettenbruch durch die Dreiecke der Modellreihe. Nun im Achsenkreis gibt es 12 bezeichnete Elemente. Also brauchen wir jetzt nur eine geometrische Entsprechung. Welche kann das sein? Die zwölf Felder des Dodekaeders können es nicht sein. Der gehört selber zu einer Modellreihe, deren einfachstes Modell der Tetraeder ist. Der besitzt aber 14 zu bezeichnende Elemente, wenn man den umschlossenen Raum nicht dazuzählt.
Nun gibt es aber eine Besonderheit. Wann ist eine Ecke eine Ecke? Eine Ecke ist nur eine Ecke, wenn es zu ihr hin immer enger wird. Um dieses feststellen zu können, muss man diesen Raum aber ausfüllen können. Er darf also noch nicht belegt sein. Wenn er schon belegt ist, gibt es zu diesem Engerwerden hin keinen Raum. Es wird nichts enger. Wir haben keine Ecke. Wenn wir von einer Grundfläche und einer Spitze ausgehen, dann kann die Spitze keine Ecke sein, wenn wir den Innenraum aus der Betrachtung weglassen und alle Seitenkanten und Seitenflächen zu dieser Spitze hinführen. Wenn wir jedoch die Grundfläche weglassen, gibt es an der Basis sehr wohl drei Ecken, weil es in der nicht gefüllten Grundfläche zu den Extrema hin immer enger wird. Ein „Außen“ gibt es nicht in diesem Modell. Nur in der Anschauung des Tetraeders als eines diskreten Objektes.
Also wir besitzen ohne die Spitze und die Grundfläche nur zwölf Elemente bei diesem speziellen „Tetraeder“. Und indem wir diesen „Tetraeder“ ohne Grundfläche und Spitze fortlaufend durch seine aneinander anschließenden Elemente konstruieren, erhalten wir auch so unsere Modelle für die Modellreihe des Achsenkreises und seine aufeinanderfolgenden Elemente Hauptfeld-Grenze-Zwischenfeld-Grenze-Hauptfeld-usw. . Der Kettenbruch, den wir brauchen, ist nicht schwer zu finden. Hierzu später. Durch den „Tetraeder“ ohne Spitze und Grundfläche erhalten wir eine Interpretationsgrundlage für die Beziehung der Zahl 2,92…… zur Zeit. Diese Zahl muss von herausragender Bedeutung zur Erklärung von physikalischen Zuständen sein.
Die Kettenbruchkonstruktion dieser Zahl könnte schon bekannt sein. Es gibt ja so viele mathematische Werke zu Kettenbrüchen. Die Einbettung in die hier aufgezeigte Systematik aber vielleicht nicht. Anders ausgedrückt: eine genauere Uhr wurde vielleicht noch niemals konstruiert. Außer es war dieselbe.
P.S.(24.3..2022, 8:20): leider habe ich obigen Gedanken nicht konsequent fortgesetzt; denn bei konsequenter Fortsetzung wäre ich auf eine Zahl unter (Pi +e) durch 2 gekommen: 2,928836889….. Das ist dann die gesuchte dritte Hauptzahl j. Dann würde (Pi +e) durch 2 einfach in das Zwischenfeld zwischen Pi und e gehören. Das wäre dann sozusagen die Zahl Pe. Die Zahl zwischen Pi und j(ji=( Pi+j)durch 2) und diejenige zwischen j und e(je=(j+e) durch 2) würden dann analog zu berechnen sein. Das wäre allerdings sehr einfach. Ist es vielleicht doch etwas anders? Ist Mathematik eine Beweiswissenschaft oder vielleicht doch eher eine Kompromisswissenschaft? Diplomatie nicht zwischen Staaten, sondern zwischen Zahlen. Warum sonst das Gleichheitszeichen? Der Kettenbruch zeigt die Lösung.
(8:54: statt Pe vielleicht besser Peu; weil die Zahl e von Eu..ler kommt; wegen der Aussprache)
(14:33 : j = 2,9288368892954454526972847488823………………, so j in der konsequenten Reihenfolge von e über Pi nach j in der Annäherung an die 3; insofern korrekt wiedergegeben)
(15:13 : (Pi+j) durch2 = ji = 3,0352147714426193455799640660809………………….;
im Vergleich dazu die Reihenfolge e, Pi und j in Annäherung an die 3 fortgesetzt: 3,035764947307106237687054405297………………..; ziemlich ähnlich; aber warum sollte die letztere Zahl zwischen Pi und j liegen?;
(Pi+e) durch 2= Peu = 2,9299372410244192369114654273161……………….;
falls alles richtig wiedergegeben)
(15:25: (j+e) durch 2 = je = 2,8235593588772453440287861101175………………………….)
(16:47: diese Ergebnisse erfordern natürlich weitere Überprüfungen; wie könnte es z.B. mit Spiralenfunktionen und der Betrachtung der Kurvenlängen aussehen?; was braucht man alles zur mathematischen Verifizierung? ; bei j bin ich mir noch sicherer als bei den Zahlen der Zwischenfelder; nur ein Anfang)
Achsenkreis der Haupt- und Zwischenzahlen und ein Zusammenhang
26.3.2022
In den folgenden zwei Grafiken auf dem abfotografierten Blatt Papier sind jene Zahlen im Achsenkreis wie beschrieben angeordnet. Dazu werden noch zur Veranschaulichung charakteristische geometrische Grundanwendungsfelder(+Rechenarten bei den Hauptzahlen) symbolartig aufgezeigt. In der zweiten Grafik wird ein Zusammenhang zwischen der Zeit(j) und den anderen schon bekannten Hauptzahlen(Pi(Werk ) und e(Raum) ) mit Hilfe jener Veranschaulichungen hergestellt. Das ist nicht Alles. Mathematik bedeutet, Möglichkeiten auszuschöpfen. Bei den Zahlen außer „Peu“ habe ich die Punkte dahinter zur Verdeutlichung der (unendlich vielen) weiteren Nachkommastellen vergessen. Je kleiner die Zahl ist, desto offener ist die zugeordnete Struktur. Den Übergang von Peu zu Pi kann man sich strukturmäßig so vorstellen, dass immer mehr Raum tendenziell unterhalb der Spaltungsspitze durch die zwei „Arme“ umarmt wird, bis sie sich treffen und die Spaltung immer glatter wird, die Spitze immer mehr nach „oben“ wandert und schließlich verschwindet. Pi ist hier die größte Zahl, weil sie durch einfachste Mittel mehr Raum ganz umschließt. Je mehr die Struktur einem Dreieck ähnelt, desto näher befindet sich die Zahl bei der Drei.
